What Is The Gcf Of 27 And 18
persisten
Dec 06, 2025 · 13 min read
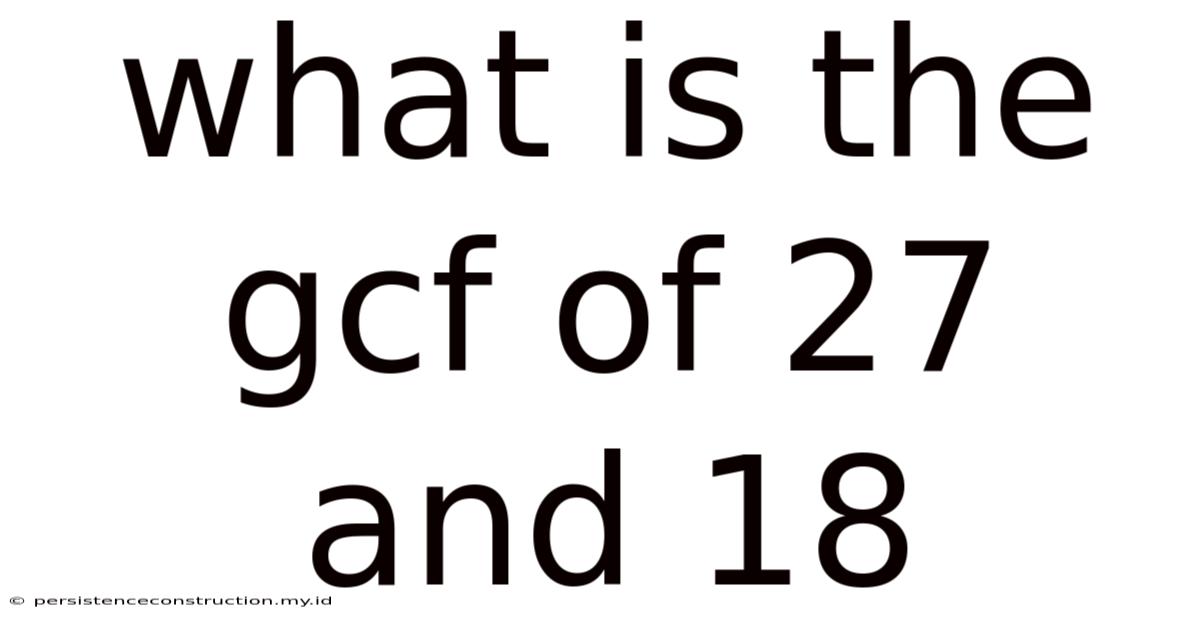
Table of Contents
Have you ever found yourself needing to divide items equally, whether it's distributing snacks among friends or organizing supplies into identical groups? The challenge often lies in finding the largest possible group size that works perfectly. This is where the concept of the greatest common factor, or GCF, comes into play. The GCF helps you find the largest number that divides evenly into two or more numbers, making equal distribution a breeze.
Imagine you're planning a bake sale. You have 27 cookies and 18 brownies, and you want to create identical treat bags. To ensure each bag has the same number of cookies and brownies without any leftovers, you need to find the greatest common factor (GCF) of 27 and 18. This article will guide you through the process of finding the GCF of these two numbers, explaining various methods and their applications, so you can confidently tackle similar problems in the future.
Main Subheading
The greatest common factor (GCF), also known as the greatest common divisor (GCD) or highest common factor (HCF), is the largest positive integer that divides two or more integers without leaving a remainder. It’s a fundamental concept in number theory with practical applications in various fields, including mathematics, computer science, and everyday problem-solving. Understanding the GCF can simplify fractions, solve algebraic equations, and optimize resource allocation.
The GCF isn't just a theoretical concept; it has real-world implications. For example, consider designing a rectangular garden bed. If you have 27 tomato plants and 18 pepper plants and want to arrange them in equal rows, the GCF will determine the maximum number of plants you can put in each row while maintaining equal distribution. This principle extends to more complex scenarios, such as scheduling tasks in project management or optimizing data storage in computer systems. Understanding the GCF is therefore a valuable skill for anyone seeking efficiency and organization in their endeavors.
Comprehensive Overview
To fully grasp the concept of the GCF, it's essential to delve into its definition, historical context, and the underlying mathematical principles.
Definition of GCF
The greatest common factor (GCF) of two or more numbers is the largest positive integer that divides each of the numbers without leaving a remainder. In simpler terms, it’s the biggest number that is a factor of all the given numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, while the factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6, with 6 being the greatest among them. Therefore, the GCF of 12 and 18 is 6.
Historical Background
The concept of the GCF has ancient roots, dating back to the early days of mathematics. The Euclidean algorithm, one of the oldest and most efficient methods for finding the GCF, was described by the Greek mathematician Euclid in his book Elements around 300 BC. Euclid's algorithm provides a systematic approach to finding the GCF of two numbers by repeatedly applying the division algorithm until the remainder is zero. This method has been used for centuries and is still widely taught and applied today. The study of number theory, which includes concepts like the GCF, has played a crucial role in the development of mathematics and related fields.
Mathematical Foundation
The GCF is closely related to the concepts of factors, multiples, and prime numbers. A factor of a number is an integer that divides the number evenly, while a multiple of a number is the product of that number and any integer. Prime numbers, which have only two factors (1 and themselves), are essential in finding the GCF using prime factorization. The prime factorization method involves expressing each number as a product of its prime factors and then identifying the common prime factors raised to the lowest power. The GCF is then the product of these common prime factors. Understanding these foundational concepts is crucial for mastering the techniques used to find the GCF.
Methods to Find the GCF
Several methods can be used to find the GCF of two or more numbers, each with its own advantages and disadvantages. The most common methods include:
- Listing Factors: This involves listing all the factors of each number and identifying the largest factor they have in common. It's straightforward but can be time-consuming for larger numbers.
- Prime Factorization: This method involves breaking down each number into its prime factors and then finding the common prime factors. It’s efficient for larger numbers but requires a good understanding of prime factorization.
- Euclidean Algorithm: This method involves repeatedly applying the division algorithm until the remainder is zero. It’s highly efficient and works well for numbers of any size.
Practical Applications
The GCF is not just a theoretical concept; it has numerous practical applications in various fields. In mathematics, it’s used to simplify fractions, solve algebraic equations, and understand number properties. In computer science, it’s used in cryptography, data compression, and algorithm optimization. In everyday life, it’s used in tasks such as dividing items equally, scheduling events, and optimizing resource allocation. For instance, if you have 48 apples and 36 oranges and want to create identical fruit baskets, the GCF of 48 and 36 (which is 12) tells you that you can create 12 baskets, each containing 4 apples and 3 oranges. Understanding and applying the GCF can greatly simplify many tasks and problems.
Trends and Latest Developments
The concept of the GCF is well-established, but its applications and methods for computation continue to evolve with advancements in technology and mathematical research.
Computational Tools and Algorithms
With the advent of computers, finding the GCF has become significantly easier and faster. Various software tools and online calculators can quickly compute the GCF of large numbers. Additionally, advancements in algorithms have led to more efficient methods for finding the GCF, especially for very large numbers used in cryptography and computer science. These algorithms often combine the principles of the Euclidean algorithm with more advanced techniques to optimize performance and reduce computational complexity.
Applications in Cryptography
The GCF plays a crucial role in cryptography, particularly in public-key cryptography systems like RSA (Rivest-Shamir-Adleman). The security of these systems relies on the difficulty of factoring large numbers into their prime factors. The GCF is used to ensure that the encryption and decryption keys are relatively prime, which is essential for the proper functioning of the cryptographic algorithms. As cryptographic techniques become more sophisticated, the use of GCF and related number-theoretic concepts becomes increasingly important.
Educational Trends
In mathematics education, there's a growing emphasis on teaching the GCF in a more intuitive and practical manner. Instead of just focusing on the mechanical steps of finding the GCF, educators are incorporating real-world examples and interactive activities to help students understand the underlying concepts. This approach aims to make the GCF more accessible and relevant to students, fostering a deeper understanding and appreciation for its applications. The use of visual aids, games, and collaborative problem-solving activities is becoming increasingly common in mathematics classrooms.
Integration with Technology
Technology is playing an increasingly important role in teaching and applying the GCF. Interactive software, online calculators, and educational apps provide students and professionals with tools to quickly and accurately find the GCF of numbers. These tools often include features such as step-by-step solutions, visual representations, and practice problems, making it easier to learn and apply the concept. Furthermore, technology enables the exploration of more complex problems involving the GCF, such as those encountered in cryptography and computer science.
Current Research and Developments
While the basic principles of the GCF are well-established, ongoing research continues to explore its properties and applications. Mathematicians are investigating the GCF in the context of more advanced number theory problems, such as those related to prime number distribution and Diophantine equations. Additionally, researchers are exploring new algorithms for computing the GCF that are optimized for specific types of numbers or computational environments. These developments contribute to a deeper understanding of the GCF and its role in mathematics and related fields.
Tips and Expert Advice
Finding the GCF of numbers can be made simpler with the right strategies and techniques. Here are some tips and expert advice to help you master this concept:
Start with Smaller Numbers
When first learning how to find the GCF, begin with smaller numbers to understand the process. For example, find the GCF of 6 and 9. The factors of 6 are 1, 2, 3, and 6, while the factors of 9 are 1, 3, and 9. The common factors are 1 and 3, and the greatest of these is 3. Therefore, the GCF of 6 and 9 is 3. Practicing with smaller numbers builds confidence and reinforces the fundamental concepts before moving on to more complex problems.
Master Prime Factorization
Prime factorization is a powerful tool for finding the GCF of larger numbers. To use this method effectively, you need to be proficient in breaking down numbers into their prime factors. For instance, to find the GCF of 48 and 60, first find their prime factorizations:
- 48 = 2 × 2 × 2 × 2 × 3 = 2⁴ × 3
- 60 = 2 × 2 × 3 × 5 = 2² × 3 × 5
Then, identify the common prime factors and their lowest powers:
- Common prime factors: 2 and 3
- Lowest powers: 2² and 3¹
Finally, multiply these together:
- GCF = 2² × 3 = 4 × 3 = 12
Utilize the Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, especially for larger numbers. The algorithm involves repeatedly applying the division algorithm until the remainder is zero. Here’s how it works:
- Divide the larger number by the smaller number and find the remainder.
- If the remainder is 0, the smaller number is the GCF.
- If the remainder is not 0, replace the larger number with the smaller number and the smaller number with the remainder.
- Repeat the process until the remainder is 0.
For example, to find the GCF of 72 and 48:
- 72 ÷ 48 = 1 remainder 24
- 48 ÷ 24 = 2 remainder 0
Since the remainder is 0, the GCF is 24.
Simplify Fractions First
When finding the GCF of fractions, simplify each fraction to its lowest terms before finding the GCF of the numerators and the LCM (least common multiple) of the denominators. This simplifies the process and reduces the chance of errors. For example, to find the GCF of 3/4 and 9/10, simplify the fractions if possible. Then find the GCF of the numerators (3 and 9), which is 3, and the LCM of the denominators (4 and 10), which is 20. The GCF of the fractions is then 3/20.
Practice Regularly
Like any mathematical skill, finding the GCF requires practice. Work through a variety of problems, starting with simpler examples and gradually increasing the difficulty. Use online resources, textbooks, and worksheets to find practice problems. The more you practice, the more comfortable and confident you will become in finding the GCF.
Use Real-World Examples
Applying the concept of the GCF to real-world scenarios can help you understand its practical significance. For example, consider dividing a set of items into equal groups, arranging plants in rows, or scheduling tasks. By seeing how the GCF is used in everyday situations, you can better appreciate its value and relevance. This can also make learning the concept more engaging and enjoyable.
Check Your Work
Always double-check your work to ensure accuracy. After finding the GCF, verify that it divides evenly into all the original numbers. If it doesn’t, you may have made a mistake in your calculations. Use a calculator or online GCF tool to verify your answers, especially when working with larger numbers. This will help you catch any errors and reinforce your understanding of the process.
FAQ
Here are some frequently asked questions about the greatest common factor (GCF):
What is the difference between GCF and LCM?
The GCF (greatest common factor) is the largest number that divides two or more numbers without leaving a remainder, while the LCM (least common multiple) is the smallest number that is a multiple of two or more numbers. In other words, the GCF is the largest factor common to the numbers, and the LCM is the smallest multiple common to the numbers.
How do I find the GCF of three or more numbers?
To find the GCF of three or more numbers, you can use the same methods as for two numbers. One approach is to find the GCF of the first two numbers, and then find the GCF of that result and the next number, and so on. For example, to find the GCF of 12, 18, and 30, first find the GCF of 12 and 18, which is 6. Then find the GCF of 6 and 30, which is 6. Therefore, the GCF of 12, 18, and 30 is 6.
Can the GCF be zero?
No, the GCF cannot be zero. By definition, the GCF is the largest positive integer that divides two or more numbers without leaving a remainder. Zero cannot be a factor because division by zero is undefined.
What if two numbers have no common factors other than 1?
If two numbers have no common factors other than 1, they are said to be relatively prime or coprime. In this case, the GCF of the two numbers is 1. For example, the numbers 8 and 9 are relatively prime because their only common factor is 1.
Is there a shortcut to finding the GCF?
Yes, the Euclidean algorithm is an efficient shortcut for finding the GCF, especially for larger numbers. It involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCF.
How is the GCF used in real life?
The GCF has many practical applications in real life. It's used in tasks such as dividing items equally, simplifying fractions, scheduling events, and optimizing resource allocation. For example, if you have 24 apples and 36 oranges and want to create identical fruit baskets, the GCF of 24 and 36 (which is 12) tells you that you can create 12 baskets, each containing 2 apples and 3 oranges.
Can the GCF be larger than the numbers you're finding it for?
No, the GCF cannot be larger than the numbers you are finding it for. By definition, the GCF is the largest factor that divides all the numbers without leaving a remainder. Therefore, it must be less than or equal to the smallest number in the set.
Conclusion
In summary, the greatest common factor (GCF) is the largest positive integer that divides two or more integers without leaving a remainder. It is a fundamental concept in number theory with practical applications in various fields, including mathematics, computer science, and everyday problem-solving. Methods for finding the GCF include listing factors, prime factorization, and the Euclidean algorithm. By understanding and applying the principles of the GCF, you can simplify fractions, solve algebraic equations, optimize resource allocation, and tackle a wide range of mathematical and practical problems.
Now that you have a comprehensive understanding of the GCF, put your knowledge to the test! Try finding the GCF of different sets of numbers using the methods discussed in this article. Share your solutions and any interesting observations in the comments below. Engage with fellow readers and deepen your understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
What Is The Gcf Of 20 And 8
Dec 06, 2025
-
How Many Glasses Of Water Is A Litre
Dec 06, 2025
-
What Is The Gcf Of 27 And 18
Dec 06, 2025
-
Lines Of Symmetry For A Hexagon
Dec 06, 2025
-
What Is 2 4 As A Decimal
Dec 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 27 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.