What Is The Gcf Of 20 And 8
persisten
Dec 06, 2025 · 10 min read
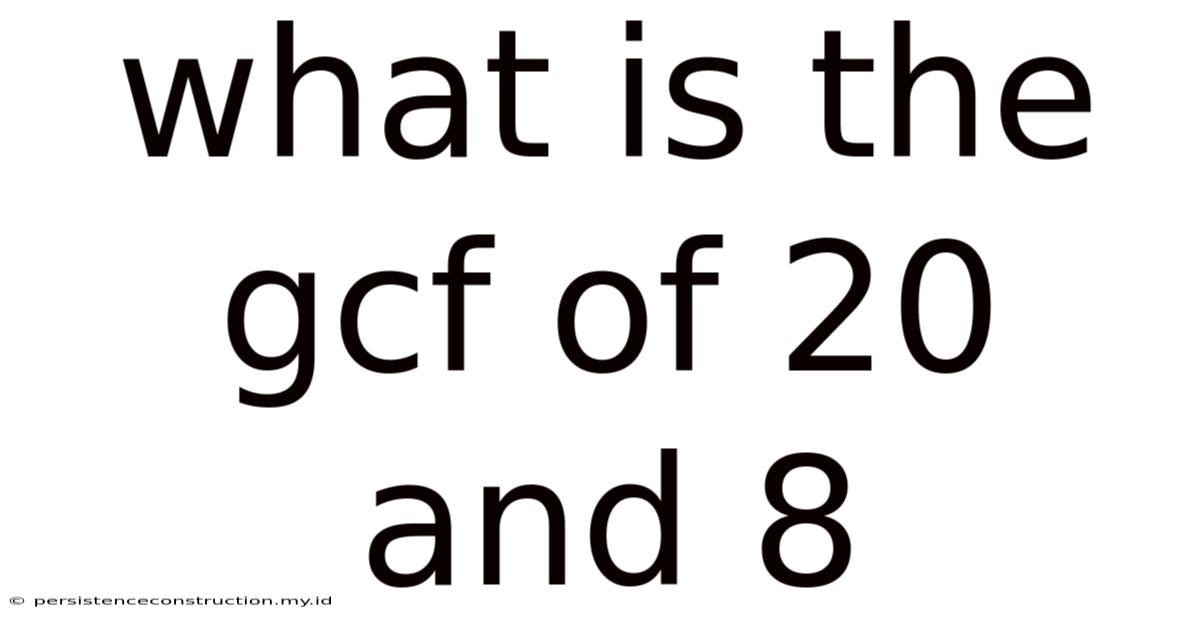
Table of Contents
Imagine you're organizing a bake sale. You have 20 cookies and 8 brownies. To make the treat bags identical, you need to figure out the largest number of cookies and brownies you can put in each bag without any leftovers. This is where the concept of the Greatest Common Factor (GCF) comes in handy.
Finding the Greatest Common Factor, or GCF, is a fundamental skill in mathematics that simplifies fractions, solves real-world problems, and forms the basis for more advanced algebraic concepts. In this article, we will explore what the GCF is, different methods to find it, and why it's so useful, using 20 and 8 as examples. So, what is the GCF of 20 and 8? The answer awaits you as you read on.
Main Subheading: Understanding the Greatest Common Factor (GCF)
The Greatest Common Factor (GCF), also known as the Highest Common Factor (HCF), is the largest positive integer that divides two or more numbers without leaving a remainder. It's a concept that bridges arithmetic and algebra, finding applications in various mathematical and everyday scenarios. Imagine you have two lengths of ribbon, one 20 inches long and another 8 inches long. What is the longest piece you can cut both ribbons into so that you use the entire length of both ribbons without any waste? The length would be the GCF of 20 and 8.
The GCF is essential for simplifying fractions, combining like terms in algebraic expressions, and solving problems related to division and distribution. Understanding how to find the GCF efficiently is a valuable skill for anyone studying math, as it helps streamline calculations and provides a deeper understanding of number relationships. In essence, the GCF is the "biggest common thread" that ties two or more numbers together in terms of divisibility.
Comprehensive Overview of the GCF
Definition and Basic Concepts
At its core, the GCF is the largest number that is a factor of two or more numbers. A factor is a number that divides another number evenly, leaving no remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because 12 can be divided evenly by each of these numbers. To find the GCF of two numbers, you need to identify the factors of each number and then determine the largest factor they have in common.
Let's consider the numbers 20 and 8. The factors of 20 are 1, 2, 4, 5, 10, and 20. The factors of 8 are 1, 2, 4, and 8. Comparing these lists, we see that the common factors of 20 and 8 are 1, 2, and 4. The largest of these common factors is 4. Therefore, the GCF of 20 and 8 is 4.
Methods for Finding the GCF
There are several methods for finding the GCF of two or more numbers, each with its own advantages depending on the size and nature of the numbers involved. The most common methods include:
-
Listing Factors: This method involves listing all the factors of each number and then identifying the largest factor they have in common, as demonstrated above. This method is suitable for smaller numbers where the factors are easy to identify.
-
Prime Factorization: Prime factorization involves expressing each number as a product of its prime factors. A prime number is a number greater than 1 that has no positive divisors other than 1 and itself (e.g., 2, 3, 5, 7, 11). To find the GCF using prime factorization, you identify the common prime factors and multiply them together.
-
Euclidean Algorithm: The Euclidean Algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCF.
Prime Factorization in Detail
Let's delve deeper into the prime factorization method. To find the GCF of 20 and 8 using prime factorization, follow these steps:
-
Prime Factorize Each Number:
- Prime factorization of 20: (20 = 2 \times 2 \times 5 = 2^2 \times 5)
- Prime factorization of 8: (8 = 2 \times 2 \times 2 = 2^3)
-
Identify Common Prime Factors:
- The common prime factor is 2.
-
Determine the Lowest Power of Common Prime Factors:
- The lowest power of 2 in the factorizations is (2^2) (from the factorization of 20).
-
Multiply the Common Prime Factors with Their Lowest Powers:
- GCF = (2^2 = 4)
Thus, the GCF of 20 and 8 is 4, as confirmed by the prime factorization method.
Euclidean Algorithm Explained
The Euclidean Algorithm is a highly efficient method, particularly useful for larger numbers where listing factors or finding prime factors can be cumbersome. Here's how to apply the Euclidean Algorithm to find the GCF of 20 and 8:
-
Divide the Larger Number by the Smaller Number:
- Divide 20 by 8: (20 = 8 \times 2 + 4)
-
Replace the Larger Number with the Smaller Number, and the Smaller Number with the Remainder:
- Now, divide 8 by the remainder 4: (8 = 4 \times 2 + 0)
-
Continue the Process Until the Remainder is Zero:
- Since the remainder is now 0, the last non-zero remainder (which is 4) is the GCF.
Therefore, the GCF of 20 and 8 is 4, consistent with the previous methods.
Importance of the GCF
Understanding and calculating the GCF is not just a mathematical exercise; it has practical applications in various fields. The GCF is crucial for:
-
Simplifying Fractions: The GCF allows you to reduce fractions to their simplest form by dividing both the numerator and the denominator by their GCF. For instance, the fraction (\frac{8}{20}) can be simplified by dividing both 8 and 20 by their GCF, which is 4. This gives (\frac{8 \div 4}{20 \div 4} = \frac{2}{5}), the simplest form of the fraction.
-
Solving Division Problems: The GCF can help in solving problems involving division, such as dividing items into equal groups. For example, if you have 20 apples and 8 oranges, the GCF (4) tells you that you can make 4 identical groups, each containing 5 apples and 2 oranges.
-
Algebraic Simplification: In algebra, the GCF is used to factor expressions and simplify equations. By identifying the GCF of the coefficients and variables, you can factor out the common term, making the expression easier to work with.
Trends and Latest Developments
While the basic concept of the GCF remains unchanged, recent trends in mathematics education emphasize the importance of understanding the underlying principles and applying them in real-world contexts. Educators are moving away from rote memorization and focusing on problem-solving skills that require a deep understanding of the GCF.
Educational Technology: Modern educational tools and software often incorporate interactive simulations and games to help students visualize and understand the GCF. These tools provide a dynamic and engaging way to learn, making the concept more accessible and enjoyable.
Real-World Applications: There's a growing emphasis on connecting mathematical concepts to real-world scenarios. For example, teachers might use examples involving resource allocation, scheduling, or design to illustrate the practical applications of the GCF.
Interdisciplinary Approaches: The GCF is also being integrated into interdisciplinary projects that combine mathematics with other subjects like art, music, and computer science. This helps students see the relevance of mathematics in various contexts and promotes a more holistic understanding.
Tips and Expert Advice for Mastering the GCF
Mastering the GCF involves not only understanding the concept but also developing efficient problem-solving strategies. Here are some tips and expert advice to help you become proficient in finding the GCF:
-
Practice Regularly: The more you practice finding the GCF, the more comfortable and confident you'll become. Start with simple examples and gradually work your way up to more complex problems. Regular practice helps reinforce the concepts and improves your speed and accuracy.
For example, try finding the GCF of different pairs of numbers like 12 and 18, 24 and 36, or 15 and 45. Each time you solve a problem, you reinforce your understanding and refine your problem-solving skills.
-
Understand the Underlying Concepts: Don't just memorize the steps for finding the GCF; make sure you understand why each step is necessary. Understanding the underlying concepts will help you apply the GCF in different contexts and solve more complex problems.
For instance, understanding that the GCF is the largest factor that divides two numbers evenly helps you appreciate why you need to find the common factors first. This understanding makes the process more intuitive and less mechanical.
-
Use Different Methods: Experiment with different methods for finding the GCF, such as listing factors, prime factorization, and the Euclidean Algorithm. Each method has its advantages and disadvantages, and choosing the right method can save you time and effort.
For small numbers, listing factors might be the easiest method. For larger numbers, the Euclidean Algorithm is often the most efficient. By being familiar with all the methods, you can choose the one that best suits the problem at hand.
-
Apply the GCF to Real-World Problems: Look for opportunities to apply the GCF in real-world scenarios. This will help you see the practical relevance of the concept and make it more engaging.
For example, you can use the GCF to solve problems related to dividing resources, scheduling events, or designing layouts. By connecting the GCF to real-world applications, you'll gain a deeper appreciation for its usefulness and versatility.
-
Check Your Answers: Always check your answers to ensure they are correct. You can do this by verifying that the GCF you found divides both numbers evenly and that there is no larger number that does so.
For example, if you find that the GCF of 20 and 8 is 4, verify that 20 ÷ 4 = 5 and 8 ÷ 4 = 2, and that there is no number larger than 4 that divides both 20 and 8 evenly. This step helps you catch any errors and reinforces your understanding of the concept.
FAQ About the Greatest Common Factor
Q: What is the difference between GCF and LCM?
A: The GCF (Greatest Common Factor) is the largest number that divides two or more numbers evenly, while the LCM (Least Common Multiple) is the smallest number that is a multiple of two or more numbers. For example, the GCF of 20 and 8 is 4, while the LCM of 20 and 8 is 40.
Q: Can the GCF be larger than the numbers themselves?
A: No, the GCF cannot be larger than the numbers themselves. The GCF is a factor of the numbers, and a factor cannot be larger than the original number.
Q: What is the GCF of two prime numbers?
A: The GCF of two different prime numbers is always 1, as prime numbers only have two factors: 1 and themselves. For example, the GCF of 7 and 11 is 1.
Q: How do you find the GCF of three or more numbers?
A: To find the GCF of three or more numbers, you can first find the GCF of two of the numbers, and then find the GCF of that result with the remaining number. For example, to find the GCF of 20, 8, and 12, you can first find the GCF of 20 and 8 (which is 4), and then find the GCF of 4 and 12 (which is 4).
Q: Is there a GCF for decimal numbers?
A: The concept of GCF is typically applied to integers (whole numbers). However, you can find a common factor for decimal numbers by converting them into fractions and then finding the GCF of the numerators and denominators.
Conclusion
In summary, the Greatest Common Factor (GCF) is the largest positive integer that divides two or more numbers without leaving a remainder. It is a fundamental concept in mathematics with applications in simplifying fractions, solving division problems, and algebraic simplification. Whether you choose to list factors, use prime factorization, or apply the Euclidean Algorithm, mastering the GCF is an invaluable skill.
Now that you have a comprehensive understanding of the GCF, put your knowledge into practice. Try solving some GCF problems on your own or explore how the GCF is used in real-world scenarios. Share your insights and experiences in the comments below and let's continue learning together!
Latest Posts
Latest Posts
-
How Many Quarts Make 1 Gallon
Dec 06, 2025
-
What Are Equivalent Fractions For 2 5
Dec 06, 2025
-
What Is The Gcf Of 20 And 8
Dec 06, 2025
-
How Many Glasses Of Water Is A Litre
Dec 06, 2025
-
What Is The Gcf Of 27 And 18
Dec 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 20 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.