20 / 2 4 5.5 2 / 4
persisten
Dec 06, 2025 · 11 min read
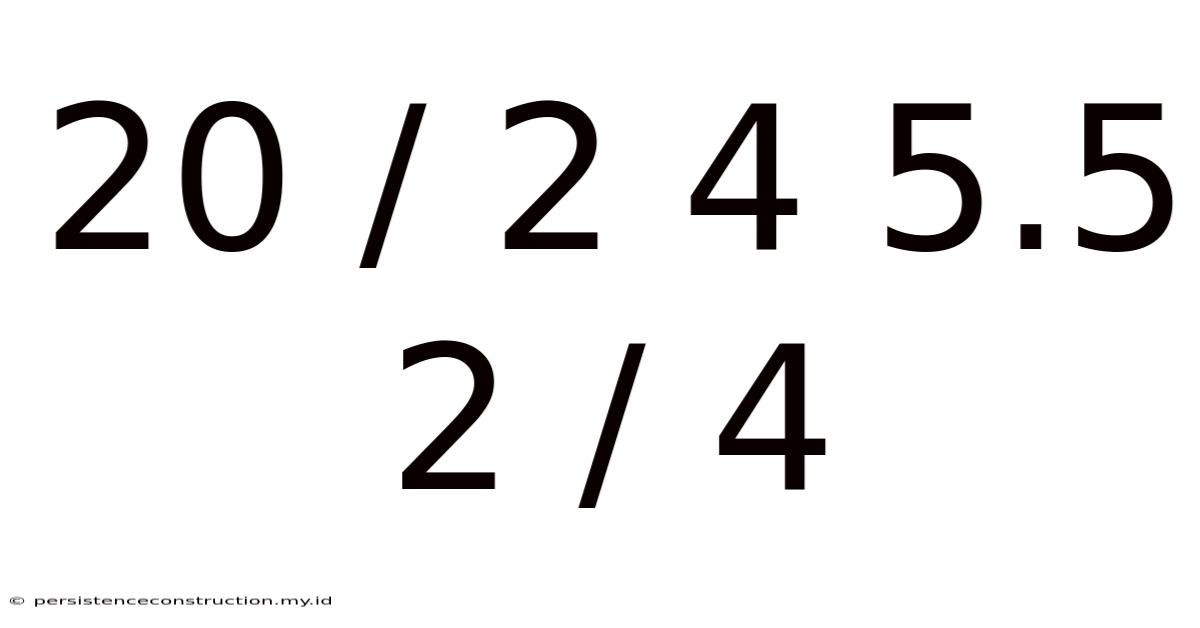
Table of Contents
Imagine you're at a bustling marketplace, trying to make sense of the day's prices. You see figures like "20 / 2" scribbled on a vendor's board, and another stall has "4 5.5" displayed prominently. Then, someone mentions "2 / 4" in passing, leaving you scratching your head, wondering how all these numbers fit together. These simple mathematical expressions, often encountered in everyday scenarios, hold the keys to understanding proportions, ratios, and basic arithmetic.
Numbers are the language of the universe, and mathematical notations like 20 / 2, 4 5.5, and 2 / 4 are fundamental tools in this language. Understanding these notations allows us to perform calculations, make comparisons, and solve problems in various contexts, from dividing resources to understanding statistical data. This article will delve deep into these expressions, unpacking their meanings, practical uses, and the underlying mathematical principles that make them so powerful.
Main Subheading
At first glance, the expressions 20 / 2, 4 5.5, and 2 / 4 might seem like isolated mathematical snippets. However, each one represents a unique operation or concept, crucial in mathematics and everyday applications.
The expression 20 / 2 represents division. In this case, it means dividing the number 20 by the number 2. Division is one of the four basic arithmetic operations, the others being addition, subtraction, and multiplication. It is used to determine how many times one number (the divisor) fits into another number (the dividend). The result of this operation is called the quotient.
Next, we have 4 5.5, which is an interesting notation because the space between the numbers might indicate different things depending on the context. Usually, in a mathematical context, it might imply multiplication, particularly in statistics or when dealing with vectors. Alternatively, in specific fields, it could represent two separate data points or measurements. Understanding the context is crucial here.
Lastly, the expression 2 / 4 represents a fraction. A fraction is a way to represent a part of a whole. In this case, 2 / 4 means 2 parts out of 4. Fractions are essential in representing proportions, ratios, and probabilities. They can be simplified or converted into decimals to provide a more intuitive understanding of their value.
Comprehensive Overview
Understanding 20 / 2, 4 5.5, and 2 / 4 requires a deeper dive into the underlying mathematical concepts. Each expression has its roots in different branches of mathematics and can be used in a multitude of ways.
20 / 2: The Essence of Division
Division, symbolized by the forward slash (/) or the division sign (÷), is the inverse operation of multiplication. It answers the question: "How many times does the divisor fit into the dividend?" In the expression 20 / 2, 20 is the dividend and 2 is the divisor. Performing the division, 20 divided by 2 equals 10. This means that 2 fits into 20 exactly 10 times.
Division is foundational in many real-world applications. For example, if you have 20 apples and want to divide them equally among 2 friends, each friend would receive 10 apples. In algebra, division is used to solve equations and simplify expressions. For example, in the equation 2x = 20, dividing both sides by 2 isolates x, giving x = 10.
Historically, division has been a crucial concept in trade, finance, and resource allocation. Ancient civilizations used division to distribute land, calculate taxes, and manage resources. The development of efficient division algorithms has been essential for advancing mathematics and science.
4 5.5: Context is Key
The expression 4 5.5 is intriguing because its meaning is heavily dependent on the context in which it is used. Let's consider the possibilities:
-
Multiplication: In some mathematical contexts, a space between two numbers implies multiplication. If this is the case, then 4 5.5 means 4 multiplied by 5.5. The result is 22. This interpretation is common in statistics when dealing with data sets or in physics when calculating quantities.
-
Separate Data Points: In data analysis or scientific measurements, 4 5.5 might represent two distinct data points. For example, 4 could be the temperature in Celsius, and 5.5 could be the humidity percentage. In this scenario, the numbers are not meant to be mathematically combined but are rather presented together for comparison or analysis.
-
Coordinates: In geometry, 4 5.5 could represent a coordinate point on a graph, where 4 is the x-coordinate and 5.5 is the y-coordinate. This is commonly used in plotting data points and visualizing relationships between variables.
-
Range: Depending on the field, it could imply a range; the intended meaning would be "4 to 5.5" (inclusive or exclusive). For example, a product's pricing range, or the possible test result interval.
Without additional context, it is impossible to definitively determine the meaning of 4 5.5. Always look for clues or additional information to understand the intended interpretation.
2 / 4: Fractions and Proportions
The expression 2 / 4 represents a fraction, where 2 is the numerator (the top number) and 4 is the denominator (the bottom number). A fraction represents a part of a whole. In this case, 2 / 4 means 2 parts out of 4.
Fractions are fundamental in representing proportions and ratios. The fraction 2 / 4 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2. This simplification yields 1 / 2. Therefore, 2 / 4 is equivalent to 1 / 2, meaning one half.
Fractions can also be converted into decimals by dividing the numerator by the denominator. In this case, 2 divided by 4 equals 0.5. Converting fractions to decimals can make it easier to compare and understand their value, especially when dealing with multiple fractions.
Fractions are widely used in everyday life. For example, in cooking, recipes often use fractions to specify the amount of ingredients needed. In finance, fractions are used to calculate interest rates and investment returns. Understanding fractions is essential for making informed decisions in various contexts.
Trends and Latest Developments
The use of mathematical expressions like 20 / 2, 4 5.5, and 2 / 4 is constantly evolving with technological advancements and changing societal needs. Here's a look at some of the current trends and latest developments:
-
Data Science and Analytics: In the field of data science, these expressions are fundamental in data manipulation and analysis. Division is used to calculate rates, ratios, and percentages. The interpretation of notations like 4 5.5 as data points is crucial in statistical analysis and machine learning. Fractions are used to represent probabilities and proportions in datasets. Data scientists use programming languages like Python and R to perform complex calculations and visualizations using these basic mathematical concepts.
-
Financial Technology (FinTech): In FinTech, mathematical expressions are used in algorithms for trading, investment analysis, and risk management. Division is used to calculate returns on investment and financial ratios. Fractions are used to represent fractional shares and interest rates. The ability to accurately and efficiently perform these calculations is essential for success in the fast-paced world of finance.
-
Artificial Intelligence (AI): AI relies heavily on mathematical foundations. Division and fractions are used in various machine learning algorithms for normalization, feature scaling, and probability calculations. The notation 4 5.5, when interpreted as coordinates or data points, is used in clustering algorithms and neural networks.
-
Education Technology (EdTech): Educational technology is leveraging digital tools to enhance the learning experience. Interactive platforms and apps use mathematical expressions to create engaging and personalized learning content. Adaptive learning systems use algorithms to adjust the difficulty level based on a student's performance, using division and fractions to assess progress and tailor instruction.
-
Cryptocurrencies and Blockchain: In the realm of cryptocurrencies and blockchain technology, mathematical expressions are at the core of cryptographic algorithms and decentralized finance (DeFi) applications. Division and fractions are used to calculate transaction fees, token distribution, and smart contract logic.
Professional Insights:
- The increasing reliance on data-driven decision-making has amplified the importance of mathematical literacy. Professionals in various fields need to be able to interpret and manipulate numerical data to make informed decisions.
- The development of new algorithms and computational tools is constantly expanding the possibilities for using mathematical expressions. From AI-powered analytics to blockchain-based finance, mathematics is driving innovation across industries.
- The integration of technology in education is making mathematics more accessible and engaging for students. Interactive simulations and virtual labs are helping students develop a deeper understanding of mathematical concepts and their applications.
Tips and Expert Advice
Mastering the use of mathematical expressions like 20 / 2, 4 5.5, and 2 / 4 requires practice and a solid understanding of the underlying concepts. Here are some practical tips and expert advice:
-
Understand the Context: Always consider the context in which the expression is used. As seen with 4 5.5, the meaning can vary significantly depending on the field or application. Look for clues or additional information to clarify the intended interpretation.
- Example: If you see 4 5.5 in a scientific paper discussing temperature and humidity, it likely represents two separate measurements. If you see it in a financial report, it might imply multiplication for calculating a certain metric.
-
Practice Regularly: The more you practice, the more comfortable you will become with these expressions. Start with simple problems and gradually increase the complexity. Use online resources, textbooks, and practice worksheets to reinforce your understanding.
- Example: Start by solving basic division problems like 20 / 2, then move on to more complex problems involving decimals and fractions. Practice converting fractions to decimals and vice versa to improve your fluency.
-
Use Visual Aids: Visual aids can be helpful for understanding fractions and proportions. Use diagrams, charts, and graphs to visualize the relationship between the numerator and the denominator.
- Example: Draw a pie chart to represent the fraction 2 / 4. Divide the pie into four equal slices, and shade two of the slices. This visual representation can help you understand that 2 / 4 is equivalent to one half.
-
Break Down Complex Problems: When faced with a complex problem involving multiple expressions, break it down into smaller, more manageable steps. Solve each step individually and then combine the results to arrive at the final answer.
- Example: If you need to calculate the total cost of a project that involves dividing resources and using fractions, start by calculating the cost of each individual resource. Then, add up the costs to get the total project cost.
-
Seek Help When Needed: Don't be afraid to ask for help if you are struggling with a particular concept. Consult with teachers, tutors, or online forums to get clarification and guidance.
- Example: If you are having trouble understanding the concept of division, ask your teacher to explain it in a different way. If you are stuck on a problem, post it on an online forum and ask for assistance.
-
Apply to Real-World Scenarios: Look for opportunities to apply these expressions in real-world scenarios. This will help you understand their practical relevance and improve your problem-solving skills.
- Example: Use fractions to calculate the amount of ingredients needed for a recipe. Use division to calculate the cost per unit of a product. Use the concept of multiplication from 4 5.5 to calculate areas, volumes, or statistical measures.
FAQ
Q: What does the expression 20 / 2 mean?
A: The expression 20 / 2 means 20 divided by 2. The result of this division is 10.
Q: What are some real-world applications of division?
A: Division is used in various real-world applications, such as dividing resources, calculating unit prices, and solving algebraic equations.
Q: How should I interpret the expression 4 5.5?
A: The interpretation of 4 5.5 depends on the context. It could mean 4 multiplied by 5.5, two separate data points, or coordinates on a graph. Always look for additional information to clarify the intended meaning.
Q: What is a fraction, and how is it represented?
A: A fraction represents a part of a whole. It is represented as a numerator (the top number) divided by a denominator (the bottom number), such as 2 / 4.
Q: How can I simplify a fraction?
A: To simplify a fraction, divide both the numerator and the denominator by their greatest common divisor. For example, 2 / 4 can be simplified to 1 / 2 by dividing both numbers by 2.
Q: How can I convert a fraction to a decimal?
A: To convert a fraction to a decimal, divide the numerator by the denominator. For example, 2 / 4 is equal to 0.5 as a decimal.
Q: Why is it important to understand mathematical expressions like these?
A: Understanding these expressions is crucial for performing calculations, making comparisons, and solving problems in various contexts, from dividing resources to understanding statistical data.
Conclusion
In conclusion, mathematical expressions like 20 / 2, 4 5.5, and 2 / 4 are fundamental tools for understanding and navigating the world around us. Whether it's dividing resources, interpreting data, or understanding proportions, these expressions provide a framework for making sense of numerical information.
By understanding the principles behind division, fractions, and contextual interpretation, you can unlock a deeper understanding of mathematics and its applications. Embrace the power of these expressions and continue to explore the world of numbers.
Call to Action: Practice using these mathematical expressions in your daily life. Solve a few practice problems, look for opportunities to apply them in real-world scenarios, and share your insights with others. By actively engaging with these concepts, you will solidify your understanding and unlock new possibilities for problem-solving and critical thinking. What are some ways you can apply 20 / 2, 4 5.5, and 2 / 4 in your own life or work? Share your ideas in the comments below!
Latest Posts
Latest Posts
-
28 Cm Is How Many Inches
Dec 06, 2025
-
How Many Yards Is A Quarter Mile
Dec 06, 2025
-
What Is 1 2 Of 1 3 4
Dec 06, 2025
-
3 Is What Percent Of 5
Dec 06, 2025
-
20 2 4 5 5 2 4
Dec 06, 2025
Related Post
Thank you for visiting our website which covers about 20 / 2 4 5.5 2 / 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.