What Is 1 2 Of 1 3 4
persisten
Dec 06, 2025 · 14 min read
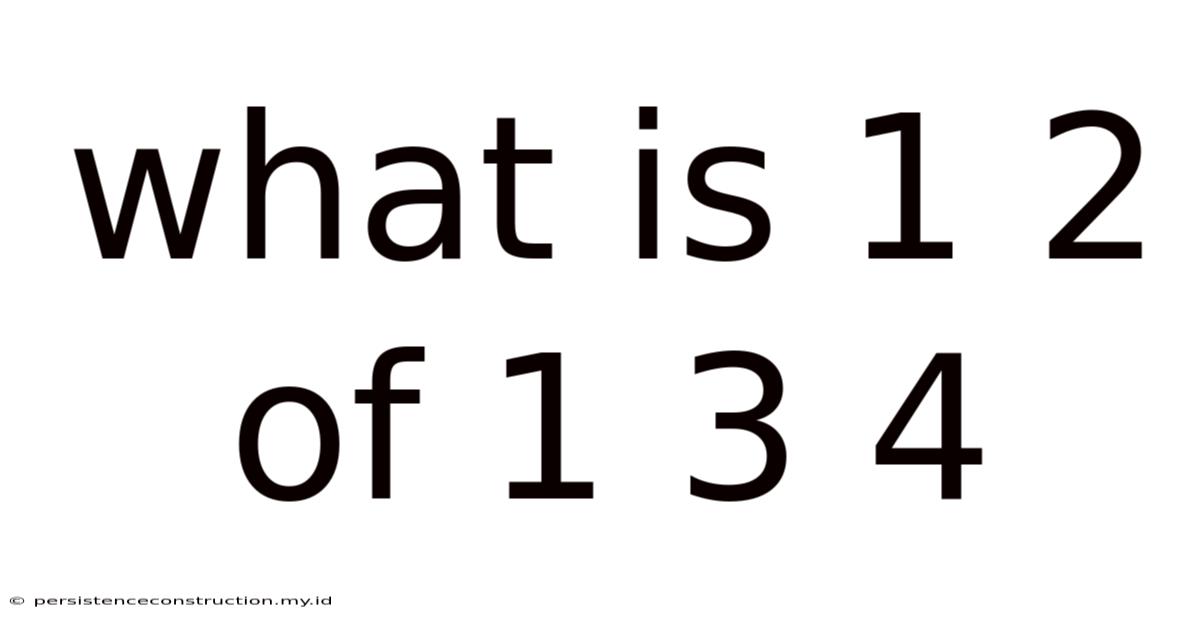
Table of Contents
Imagine you're baking a cake for a friend's birthday. The recipe calls for a specific amount of flour, but you only have measuring cups that are fractions of the size you need. Suddenly, you're faced with figuring out what "1/2 of 1 3/4" actually means in terms of how much flour to scoop. This everyday scenario highlights the practical importance of understanding how to work with fractions, especially when dealing with mixed numbers.
The ability to solve "what is 1/2 of 1 3/4" isn't just about getting the right answer on a math test; it's about developing a fundamental skill that applies to countless situations in daily life. Whether it's adjusting recipes, calculating distances, or figuring out discounts, knowing how to multiply and divide fractions accurately is essential. This article will guide you through the process step-by-step, ensuring you grasp the underlying concepts and can confidently tackle similar problems in the future.
Understanding the Basics of Fractions
Fractions are a way of representing parts of a whole. They consist of two numbers: the numerator (the number on top) and the denominator (the number on the bottom). The denominator tells you how many equal parts the whole is divided into, and the numerator tells you how many of those parts you have. For example, in the fraction 1/4, the whole is divided into four equal parts, and we have one of those parts.
A proper fraction is a fraction where the numerator is less than the denominator (e.g., 2/3). An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4). A mixed number is a combination of a whole number and a proper fraction (e.g., 1 1/2). In the question "what is 1/2 of 1 3/4", we are dealing with both a proper fraction (1/2) and a mixed number (1 3/4).
To effectively answer "what is 1/2 of 1 3/4", we need to understand how to convert mixed numbers into improper fractions, and how to multiply fractions. Converting a mixed number to an improper fraction involves multiplying the whole number by the denominator of the fraction, adding the numerator, and then placing the result over the original denominator. For instance, 1 3/4 becomes (1 * 4 + 3) / 4 = 7/4. Multiplying fractions is straightforward: simply multiply the numerators together and the denominators together.
Fractions have been used for thousands of years, dating back to ancient civilizations like the Egyptians and Babylonians. The Egyptians used fractions extensively in their measurements and calculations, primarily using unit fractions (fractions with a numerator of 1). The Babylonians, on the other hand, used a base-60 number system, which led to the development of more complex fractions. The concept of fractions gradually evolved over time, with different cultures contributing to its development and notation. The modern notation we use today is largely attributed to the Arabs and Europeans during the Middle Ages.
The idea of finding a fraction "of" another number implies multiplication. In mathematical terms, "of" is often synonymous with multiplication. Therefore, "1/2 of 1 3/4" means "1/2 multiplied by 1 3/4." This understanding is crucial to solving the problem accurately. By converting the mixed number to an improper fraction and then multiplying, we can find the answer. This process allows us to determine the portion of 1 3/4 that 1/2 represents, providing a clear and concise solution to the question.
Comprehensive Guide to Solving "What is 1/2 of 1 3/4"
To accurately determine what 1/2 of 1 3/4 is, a systematic approach is required. This involves converting the mixed number to an improper fraction, multiplying the fractions, and simplifying the result if necessary. Each step is crucial to ensure the correct answer.
Step 1: Convert the Mixed Number to an Improper Fraction
As mentioned earlier, the mixed number 1 3/4 needs to be converted into an improper fraction. To do this, multiply the whole number (1) by the denominator (4) and add the numerator (3). This gives us (1 * 4) + 3 = 7. Place this result over the original denominator (4) to get the improper fraction 7/4. Therefore, 1 3/4 is equivalent to 7/4.
Step 2: Multiply the Fractions
Now that we have 1/2 and 7/4, we can multiply them. To multiply fractions, multiply the numerators together and the denominators together. So, (1/2) * (7/4) = (1 * 7) / (2 * 4) = 7/8. This means that 1/2 of 7/4 is 7/8.
Step 3: Simplify the Result (if necessary)
In this case, the fraction 7/8 is already in its simplest form because 7 and 8 do not share any common factors other than 1. If the resulting fraction could be simplified, you would divide both the numerator and the denominator by their greatest common factor (GCF).
Therefore, 1/2 of 1 3/4 is 7/8.
Alternative Methods
While the above method is the standard approach, there are alternative ways to visualize and solve this problem. One method is to break down the mixed number into its components and distribute the multiplication. For example, 1/2 of 1 3/4 can be seen as 1/2 of (1 + 3/4). This can be solved as (1/2 * 1) + (1/2 * 3/4) = 1/2 + 3/8. To add these fractions, we need a common denominator, which is 8. So, 1/2 becomes 4/8, and the expression becomes 4/8 + 3/8 = 7/8. This method reinforces the understanding of the distributive property and provides a different perspective on the problem.
Another visual method involves using diagrams or pie charts to represent the fractions. Draw a pie chart representing 1 3/4. Divide it into four equal parts (quarters), and you'll have one whole pie and three quarters of another. Now, take half of this entire amount. Half of the whole pie is 1/2, and half of the three quarters is 3/8. Adding these together (1/2 + 3/8) again gives us 7/8. This visual approach can be particularly helpful for learners who benefit from visual aids.
Understanding these different methods not only helps in solving the problem "what is 1/2 of 1 3/4" but also enhances your overall understanding of fractions and their applications. It's important to practice these methods with various examples to build confidence and fluency.
Current Trends and Insights on Fraction Education
Fraction education has seen significant shifts in recent years, driven by research in mathematics education and the increasing recognition of the importance of conceptual understanding. Traditional methods often focused on rote memorization of rules and procedures, which, while providing quick answers, often failed to foster deep understanding. Modern approaches emphasize the importance of building a strong foundation of conceptual knowledge before introducing abstract algorithms.
One of the key trends is the use of visual and manipulative aids to help students understand fractions. Tools like fraction bars, pie charts, and number lines are used to represent fractions concretely, making it easier for students to grasp the underlying concepts. These tools help students visualize fractions as parts of a whole, compare fractions, and perform operations like addition and subtraction more intuitively. This hands-on approach is particularly effective in the early stages of learning, as it allows students to build a mental model of fractions that they can later use to solve more complex problems.
Another trend is the emphasis on real-world applications of fractions. Instead of presenting fractions in isolation, educators are increasingly using contextual problems that relate to students' lives. For example, problems involving cooking, measuring, or sharing are used to illustrate the relevance of fractions and motivate students to learn. This approach helps students see fractions as practical tools that can be used to solve everyday problems, rather than abstract mathematical concepts.
Moreover, there's a growing recognition of the importance of addressing common misconceptions about fractions. Many students struggle with fractions because they apply whole-number thinking to fractional contexts. For example, they may believe that a larger denominator means a larger fraction, or that fractions must always be less than 1. Educators are now using targeted interventions to address these misconceptions and help students develop a more accurate understanding of fractions. These interventions often involve using visual models and providing opportunities for students to explain their reasoning and justify their answers.
Professional insights from mathematics educators suggest that a balanced approach is most effective. This involves combining conceptual understanding with procedural fluency. Students need to understand the underlying concepts of fractions, but they also need to be able to perform operations accurately and efficiently. This requires a combination of hands-on activities, explicit instruction, and ample practice. It's also important to provide students with opportunities to solve challenging problems that require them to apply their knowledge in creative ways. By fostering both conceptual understanding and procedural fluency, educators can help students develop a deep and lasting understanding of fractions that will serve them well in their future studies and careers.
Practical Tips and Expert Advice for Mastering Fractions
Mastering fractions requires more than just memorizing rules; it involves developing a deep understanding of the concepts and practicing regularly. Here are some practical tips and expert advice to help you or your students improve your skills with fractions:
Tip 1: Use Visual Aids Regularly
Visual aids are incredibly helpful for understanding fractions, especially for those who are new to the concept. Fraction bars, pie charts, and number lines can make abstract ideas more concrete. For example, when solving "what is 1/2 of 1 3/4," draw a pie chart representing 1 3/4. Divide the whole into four equal parts and shade one whole and three parts. Then, shade half of the entire figure to visually represent 1/2 of 1 3/4. This visual representation can help you see the answer (7/8) more clearly.
Tip 2: Relate Fractions to Real-World Scenarios
Connect fractions to everyday situations to make them more relatable. Cooking is an excellent example. If a recipe calls for 1 3/4 cups of flour and you want to halve the recipe, you're essentially solving "what is 1/2 of 1 3/4." Similarly, when splitting a pizza or sharing a cake, you're dealing with fractions. By relating fractions to these scenarios, you can see their practical applications and understand them better.
Tip 3: Practice Converting Between Mixed Numbers and Improper Fractions
Fluency in converting between mixed numbers and improper fractions is crucial for performing operations with fractions. Practice this skill regularly by converting various mixed numbers into improper fractions and vice versa. For example, convert 2 1/3 to an improper fraction: (2 * 3) + 1 = 7, so 2 1/3 = 7/3. Then, practice converting improper fractions back to mixed numbers. This will help you become more comfortable with these conversions and make it easier to solve problems involving fractions.
Tip 4: Understand the Concept of "Of" as Multiplication
Remember that in mathematics, "of" often means multiplication. When you see a problem like "what is 1/2 of 1 3/4," think of it as "1/2 multiplied by 1 3/4." This understanding will help you translate word problems into mathematical expressions and solve them correctly. Practice translating different phrases involving "of" into multiplication problems to reinforce this concept.
Tip 5: Break Down Complex Problems into Smaller Steps
When faced with complex problems involving fractions, break them down into smaller, more manageable steps. For example, if you need to find 2/3 of 3 1/2, first convert 3 1/2 to an improper fraction (7/2), and then multiply 2/3 by 7/2. This step-by-step approach can make the problem less intimidating and reduce the likelihood of errors.
Tip 6: Seek Help and Resources When Needed
Don't hesitate to seek help from teachers, tutors, or online resources if you're struggling with fractions. There are many excellent websites and videos that can provide additional explanations and examples. Additionally, working with a tutor or study group can provide personalized support and help you address your specific challenges.
By following these tips and seeking help when needed, you can improve your skills with fractions and gain confidence in your ability to solve problems involving them. Remember that practice is key, so make sure to work on fractions regularly to reinforce your understanding and build fluency.
FAQ: Frequently Asked Questions About Fractions
Q: Why is it important to understand fractions?
A: Understanding fractions is crucial because they are used in many aspects of daily life, from cooking and baking to measuring and financial calculations. A solid grasp of fractions also forms a foundation for more advanced mathematical concepts, such as algebra and calculus.
Q: What is the difference between a proper and an improper fraction?
A: A proper fraction is a fraction where the numerator is less than the denominator (e.g., 2/3), while an improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4).
Q: How do you convert a mixed number to an improper fraction?
A: To convert a mixed number to an improper fraction, multiply the whole number by the denominator of the fraction, add the numerator, and then place the result over the original denominator. For example, to convert 1 3/4 to an improper fraction, calculate (1 * 4) + 3 = 7, and then place 7 over the denominator 4, resulting in 7/4.
Q: How do you multiply fractions?
A: To multiply fractions, multiply the numerators together and the denominators together. For example, (1/2) * (3/4) = (1 * 3) / (2 * 4) = 3/8.
Q: What does "of" mean in math problems involving fractions?
A: In math problems, "of" often means multiplication. For example, "1/2 of 1 3/4" means "1/2 multiplied by 1 3/4."
Q: How do you simplify a fraction?
A: To simplify a fraction, divide both the numerator and the denominator by their greatest common factor (GCF). For example, to simplify 4/8, the GCF of 4 and 8 is 4. Dividing both the numerator and the denominator by 4 gives us 1/2.
Q: Can you use a calculator to solve fraction problems?
A: Yes, many calculators can perform operations with fractions. However, it's important to understand the underlying concepts so you can check your answers and solve problems without a calculator if necessary.
Q: What are some common mistakes people make when working with fractions?
A: Common mistakes include forgetting to convert mixed numbers to improper fractions before multiplying, incorrectly adding or subtracting fractions without a common denominator, and misinterpreting the meaning of "of" in word problems.
Q: Where can I find more resources to learn about fractions?
A: There are many online resources, including websites like Khan Academy and Mathway, that offer lessons and practice problems on fractions. Additionally, textbooks, workbooks, and tutoring services can provide additional support.
Conclusion
In summary, understanding how to solve problems like "what is 1/2 of 1 3/4" is fundamental to mastering fractions. This involves converting mixed numbers to improper fractions, multiplying the fractions, and simplifying the result. By using visual aids, relating fractions to real-world scenarios, and practicing regularly, you can develop a strong understanding of fractions and improve your problem-solving skills. Remember that consistent practice and a solid grasp of the basic concepts are key to success.
Now that you have a comprehensive understanding of how to work with fractions, take the next step and apply this knowledge to solve various problems. Practice converting mixed numbers, multiplying fractions, and simplifying results. Share this article with friends or classmates who may also benefit from it. Leave a comment below with any questions or insights you have about fractions. By actively engaging with the material, you can reinforce your understanding and build confidence in your ability to tackle fraction-related challenges.
Latest Posts
Latest Posts
-
How Many Kg Is 160 Pounds
Dec 06, 2025
-
How Many Weeks Is 26 Days
Dec 06, 2025
-
How Many Times Does 15 Go Into 135
Dec 06, 2025
-
How Do You Convert A Fraction To A Whole Number
Dec 06, 2025
-
28 Cm Is How Many Inches
Dec 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2 Of 1 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.