What Is 1/4 As A Percent
persisten
Dec 06, 2025 · 11 min read
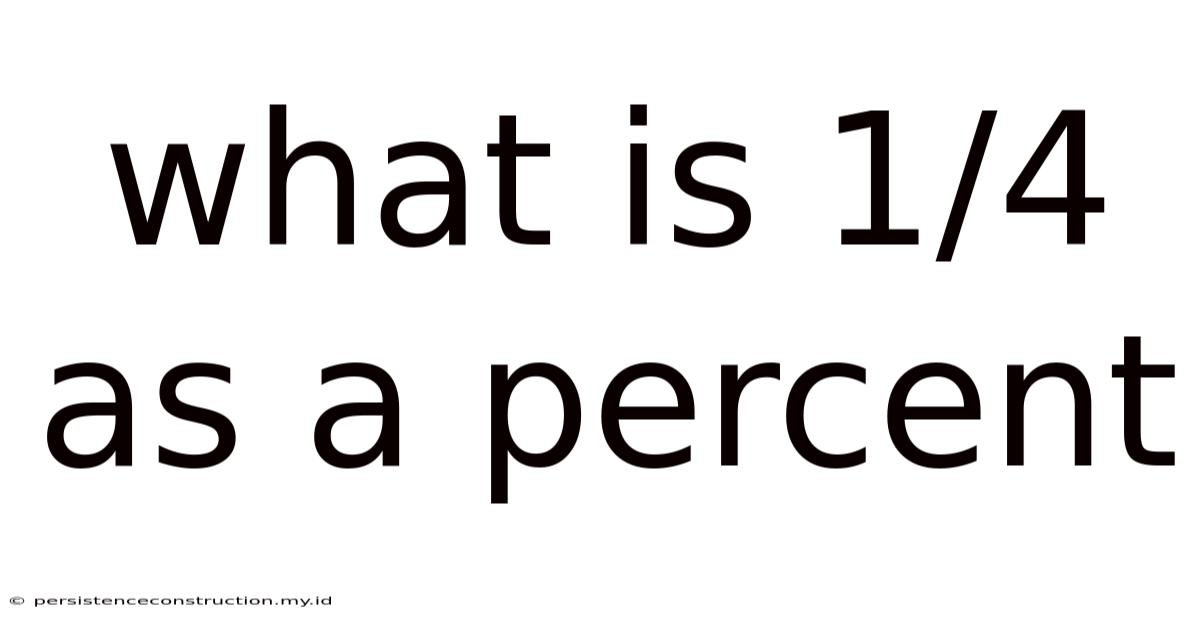
Table of Contents
Imagine you're dividing a pie into four equal slices and someone asks you what percentage of the whole pie one slice represents. This simple question illustrates the core concept of converting fractions to percentages. Understanding how to express fractions like 1/4 as a percentage is not just a mathematical exercise; it's a practical skill that helps in everyday situations, from calculating discounts to understanding statistics.
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications. At its heart, a percentage is simply a way of expressing a number as a fraction of 100. Therefore, learning to express 1/4 as a percent, and other fractions, allows us to better interpret and compare different quantities. This skill is crucial in various fields, including finance, economics, science, and even everyday tasks like cooking or shopping. By mastering this conversion, we gain a more intuitive understanding of proportions and ratios, enabling us to make informed decisions and solve problems more effectively.
Main Subheading
Converting fractions to percentages is an essential mathematical skill that bridges the gap between different numerical representations. A fraction represents a part of a whole, while a percentage expresses a number as a fraction of 100. Understanding how to convert 1/4 to a percentage is a common and practical exercise that helps in numerous real-life situations.
The process involves transforming the fraction into an equivalent fraction with a denominator of 100, or by multiplying the fraction by 100 and adding the percent symbol (%). This skill is fundamental in various areas, including finance, statistics, and everyday problem-solving. Knowing how to perform this conversion efficiently and accurately can significantly enhance one's ability to interpret and analyze data, make informed decisions, and understand proportional relationships.
Comprehensive Overview
The concept of converting fractions to percentages is rooted in the idea of expressing proportions in a standardized format. A percentage is a way of representing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." This standardized format allows for easy comparison and understanding of different proportions.
To convert a fraction to a percentage, the basic principle involves scaling the fraction so that its denominator becomes 100. Once the denominator is 100, the numerator directly represents the percentage. This is because the numerator then indicates how many parts out of 100 the fraction represents. For example, if a fraction is converted to 25/100, it means 25 out of 100, which is expressed as 25%.
The mathematical foundation for this conversion lies in the properties of fractions and proportions. A fraction represents a division of two numbers, and to maintain the fraction's value while changing its denominator, you must multiply both the numerator and the denominator by the same factor. This principle ensures that the proportion remains constant, even as the numerical representation changes.
History
The use of percentages dates back to ancient Rome, where calculations were often made in terms of fractions of 100. However, the modern concept of percentages became more formalized during the Renaissance. As trade and commerce expanded, there was an increasing need for a standardized way to express proportions and ratios. This led to the widespread adoption of percentages as a convenient and universally understood tool for numerical representation.
Over time, percentages have become an integral part of various fields, including finance, statistics, economics, and science. They are used to express rates, ratios, changes, and distributions, providing a common language for quantitative analysis. The development of calculators and computers has further simplified the process of converting fractions to percentages, making it even more accessible and practical for everyday use.
Method
To convert 1/4 to a percentage, we follow a simple and straightforward process. There are two primary methods to achieve this conversion:
-
Direct Conversion: This method involves finding an equivalent fraction with a denominator of 100. To do this, we determine what number we need to multiply the denominator (4) by to get 100. In this case, 4 multiplied by 25 equals 100. Therefore, we multiply both the numerator and the denominator of 1/4 by 25:
(1 * 25) / (4 * 25) = 25/100
Since 25/100 means "25 out of 100," we can directly express this as 25%.
-
Multiplication by 100: This method involves multiplying the fraction by 100 and adding the percent symbol (%). This works because multiplying by 100 effectively scales the fraction to represent how many parts it would have if the whole were 100.
(1/4) * 100 = 25
Adding the percent symbol, we get 25%.
Both methods are mathematically sound and lead to the same result. The choice between them often depends on personal preference and the specific context of the problem. The direct conversion method can be more intuitive for those who prefer to work with equivalent fractions, while the multiplication by 100 method may be quicker for those comfortable with algebraic manipulation.
Trends and Latest Developments
In recent years, the use of percentages has remained a fundamental tool in various fields, but the ways they are applied and interpreted have evolved. With the increasing availability of data and the rise of data analytics, percentages are now more commonly used in complex analyses and visualizations. Understanding percentages is crucial for interpreting data trends, making informed decisions, and communicating findings effectively.
One notable trend is the increased emphasis on understanding the context behind percentages. It's not enough to simply know that a quantity is 25%; it's also important to understand what that 25% represents in relation to the whole and what factors might influence that percentage. This contextual understanding is particularly important in fields like finance and economics, where percentages are used to express rates of return, inflation, and other key indicators.
Opinions
Public opinion on the use of percentages is generally positive, as they provide a clear and easily understandable way to express proportions. However, there are also some common misconceptions and criticisms. One common mistake is to assume that a percentage change is always symmetrical. For example, if a price increases by 25% and then decreases by 25%, the final price is not the same as the original price. This is because the 25% decrease is calculated based on the higher price after the increase.
Another criticism is that percentages can sometimes be used to mislead or manipulate data. For example, a company might claim a "100% improvement" without specifying the baseline or the scope of the improvement. It's important to critically evaluate the data and the context behind percentages to avoid being misled.
Professional Insights
From a professional perspective, percentages are an indispensable tool for quantitative analysis and communication. In finance, percentages are used to calculate returns on investment, interest rates, and profit margins. In statistics, they are used to express probabilities, confidence intervals, and statistical significance. In marketing, they are used to measure market share, conversion rates, and customer satisfaction.
However, professionals also recognize the limitations and potential pitfalls of using percentages. It's important to be aware of the base rate fallacy, which is the tendency to ignore base rates (the underlying prevalence of a condition) when evaluating probabilities. For example, if a test has a 99% accuracy rate, it might seem very reliable. However, if the condition being tested for is rare, the probability of a positive result being a false positive can be surprisingly high.
To use percentages effectively, professionals emphasize the importance of clear communication, transparency, and contextual understanding. When presenting data, it's important to provide enough information for the audience to understand the underlying numbers and the assumptions behind the calculations. It's also important to be aware of potential biases and limitations and to avoid using percentages to mislead or manipulate data.
Tips and Expert Advice
Converting fractions to percentages is a practical skill that can be enhanced with a few tips and expert advice. Here are some strategies to improve your understanding and application of this concept:
Master Basic Fractions
A strong foundation in basic fractions is essential for converting them to percentages. Familiarize yourself with common fractions like 1/2, 1/3, 1/4, 1/5, and their decimal and percentage equivalents. Knowing these conversions by heart can save time and improve accuracy.
For example, knowing that 1/2 is equal to 50% and 1/4 is equal to 25% allows you to quickly estimate and check your calculations. This knowledge also helps in understanding more complex fractions and their relationships to percentages. Practice converting these basic fractions regularly to reinforce your understanding.
Use Benchmarks
Benchmarks are reference points that can help you estimate and calculate percentages more easily. Common benchmarks include 10%, 25%, 50%, and 75%. These benchmarks can be used to break down more complex percentages into simpler parts.
For instance, if you need to calculate 35% of a number, you can break it down into 25% + 10%. If you know that 10% is simply the number divided by 10, and 25% is one-fourth of the number, you can quickly calculate the total. This approach is particularly useful for mental calculations and estimations.
Understand the Context
Always consider the context in which you are using percentages. A percentage is meaningless without understanding what it represents. Ask questions like: What is the whole that the percentage is based on? What are the units of measurement? What are the potential sources of error or bias?
For example, if a company claims a 50% increase in sales, it's important to know what the sales were before the increase and what factors might have contributed to the increase. Understanding the context helps you interpret the percentage accurately and avoid drawing misleading conclusions.
Practice Regularly
Like any skill, converting fractions to percentages requires regular practice. Work through a variety of examples and problems to reinforce your understanding and improve your speed and accuracy.
Use online resources, textbooks, or worksheets to find practice problems. Start with simple fractions and gradually work your way up to more complex ones. Pay attention to common mistakes and learn from them. Regular practice will build your confidence and make you more proficient at converting fractions to percentages.
Use Technology Wisely
While it's important to understand the underlying principles of converting fractions to percentages, technology can be a useful tool for checking your work and solving more complex problems. Calculators and spreadsheets can quickly convert fractions to percentages, allowing you to focus on the interpretation and application of the results.
However, be careful not to rely too heavily on technology. Make sure you understand the process and can perform the conversion manually. This will help you develop a deeper understanding of the concept and avoid making mistakes when technology is not available.
FAQ
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, you can either find an equivalent fraction with a denominator of 100 or multiply the fraction by 100 and add the percent symbol (%). For example, to convert 1/4 to a percentage, you can multiply 1/4 by 100, which equals 25%. So, 1/4 is equal to 25%.
Q: Why is it important to know how to convert fractions to percentages?
A: Knowing how to convert fractions to percentages is important because it allows you to easily compare and understand different proportions. Percentages are a standardized way of expressing ratios, making it easier to interpret data, make informed decisions, and solve problems in various fields.
Q: What are some common mistakes to avoid when converting fractions to percentages?
A: One common mistake is to forget to multiply by 100 when using the multiplication method. Another mistake is to not simplify the fraction before converting it to a percentage. Always ensure that you have a clear understanding of the fraction and the context in which you are using it.
Q: Can all fractions be easily converted to percentages?
A: Yes, all fractions can be converted to percentages, but some may result in repeating decimals. In such cases, you may need to round the percentage to a certain number of decimal places for practical purposes.
Q: How can I improve my skills in converting fractions to percentages?
A: To improve your skills, practice regularly with different types of fractions, use benchmarks to estimate percentages, and always understand the context in which you are using percentages. Additionally, use technology wisely to check your work and solve more complex problems.
Conclusion
In summary, understanding how to express 1/4 as a percent, and converting fractions to percentages is a fundamental mathematical skill with wide-ranging applications. By mastering the methods of direct conversion and multiplication by 100, you can confidently transform fractions into percentages and interpret them in various contexts. Remember to practice regularly, use benchmarks, and always consider the context to enhance your understanding and accuracy.
Now that you've gained a solid understanding of how to convert fractions to percentages, take the next step and apply this knowledge in your daily life. Whether you're calculating discounts while shopping, analyzing financial data, or understanding statistics, the ability to convert fractions to percentages will empower you to make informed decisions and solve problems more effectively. Share this article with friends and colleagues who might benefit from this knowledge, and continue to explore other mathematical concepts to expand your skills and understanding.
Latest Posts
Latest Posts
-
60 Days Is How Many Weeks
Dec 06, 2025
-
4 4 5 As A Decimal
Dec 06, 2025
-
What Is 15 Hours From Now
Dec 06, 2025
-
What Is 1 4 As A Percent
Dec 06, 2025
-
Is Cosine The Derivative Of Sine
Dec 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.